Implements a linear saturation-capillary pressure relation. More...

#include <dumux/material/fluidmatrixinteractions/2p/regularizedlinearmaterial.hh>

Description

template<class ScalarT, class ParamsT = RegularizedLinearMaterialParams<ScalarT>>
class Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >

Implements a linear saturation-capillary pressure relation.

The entry pressure is reached at \(\mathrm{\overline{S}_w = 1}\), the maximum capillary pressure is observed at \(\mathrm{\overline{S}_w = 0}\).

It may seem strange to regularize a linear material, here comes the rationale:

The relative permeabilities are 0 or 1 outside of the range of effective saturation. However, the transition between the linearly changing and the constant part is not smooth but with a kink. The Newton scheme does not like that. Therefore a smooth transition is accomplished by interpolating these regions with a spline.

An example of the regularization of the relative permeability is shown below:

See also: LinearMaterial

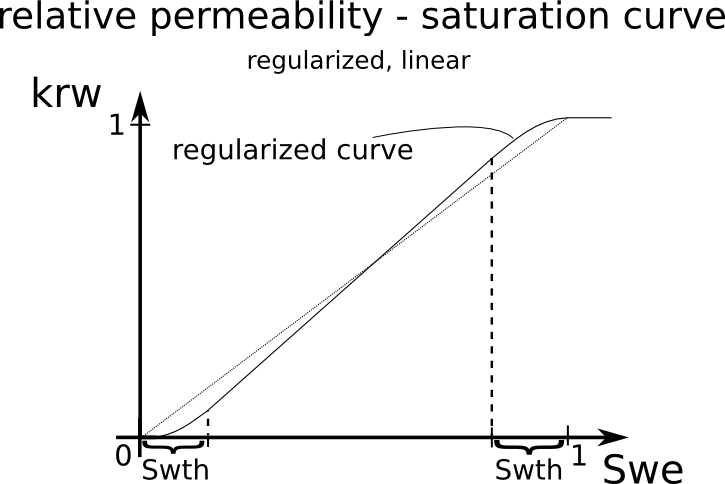
Public Types
using	Params = ParamsT

using	Scalar = typename Params::Scalar

Static Public Member Functions
static Scalar	pc (const Params &params, Scalar swe)
	The linear capillary pressure-saturation curve. More...

static Scalar	sw (const Params &params, Scalar pc)
	The saturation-capillary pressure curve. More...

static Scalar	endPointPc (const Params &params)
	The capillary pressure at Swe = 1.0 also called end point capillary pressure. More...

static Scalar	dpc_dswe (const Params &params, Scalar swe)
	Returns the partial derivative of the capillary pressure to the effective saturation. More...

static Scalar	dswe_dpc (const Params &params, Scalar pc)
	Returns the partial derivative of the effective saturation to the capillary pressure. More...

static Scalar	krw (const Params &params, Scalar swe)
	The relative permeability for the wetting phase. More...

static Scalar	krn (const Params &params, Scalar swe)
	The relative permeability for the nonwetting phase. More...

Member Typedef Documentation

◆ Params

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

using Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::Params = ParamsT

◆ Scalar

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

using Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::Scalar = typename Params::Scalar

Member Function Documentation

◆ dpc_dswe()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::dpc_dswe	(	const Params &	params,
		Scalar	swe
	)

inlinestatic

Returns the partial derivative of the capillary pressure to the effective saturation.

This is equivalent to \(\mathrm{ \frac{\partial p_C}{\partial \overline{S}_w} = - (p_{C,max} - p_{C,min}) }\)

Parameters

swe	Effective saturation of the wetting phase \(\mathrm{\overline{S}_w}\) conversion from absolute saturation happened in EffToAbsLaw.
params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.

◆ dswe_dpc()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::dswe_dpc	(	const Params &	params,
		Scalar	pc
	)

inlinestatic

Returns the partial derivative of the effective saturation to the capillary pressure.

Parameters

pc	Capillary pressure \(\mathrm{p_C}\) in \(\mathrm{[Pa]}\)
params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.

◆ endPointPc()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::endPointPc ( const Params & params )

inlinestatic

The capillary pressure at Swe = 1.0 also called end point capillary pressure.

Parameters

params A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.

◆ krn()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::krn	(	const Params &	params,
		Scalar	swe
	)

inlinestatic

The relative permeability for the nonwetting phase.

Parameters

params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.
swe	Effective saturation of the wetting phase \(\mathrm{\overline{S}_w}\) conversion from absolute saturation happened in EffToAbsLaw.

◆ krw()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::krw	(	const Params &	params,
		Scalar	swe
	)

inlinestatic

The relative permeability for the wetting phase.

Parameters

params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.
swe	Effective saturation of the wetting phase \(\mathrm{\overline{S}_w}\) conversion from absolute saturation happened in EffToAbsLaw.

◆ pc()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::pc	(	const Params &	params,
		Scalar	swe
	)

inlinestatic

The linear capillary pressure-saturation curve.

This material law is linear: \(\\mathrm{ p_C = (1 - \overline{S}_w) (p_{C,max} - p_{C,entry}) + p_{C,entry} }\)

Parameters

swe	Effective saturation of the wetting phase \(\mathrm{\overline{S}_w}\) conversion from absolute saturation happened in EffToAbsLaw.
params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.

◆ sw()

template<class ScalarT , class ParamsT = RegularizedLinearMaterialParams<ScalarT>>

static Scalar Dumux::RegularizedLinearMaterial< ScalarT, ParamsT >::sw	(	const Params &	params,
		Scalar	pc
	)

inlinestatic

The saturation-capillary pressure curve.

This is the inverse of the capillary pressure-saturation curve: \(\mathrm{ S_w = 1 - \frac{p_C - p_{C,entry}}{p_{C,max} - p_{C,entry}} }\)

Parameters

pc	Capillary pressure \(\mathrm{p_C}\) in \(\mathrm{[Pa]}\)
params	A container object that is populated with the appropriate coefficients for the respective law. Therefore, in the (problem specific) spatialParameters first, the material law is chosen, and then the params container is constructed accordingly. Afterwards the values are set there, too.

Returns: The effective saturation of the wetting phase \(\mathrm{\overline{S}_w}\)

The documentation for this class was generated from the following file:

regularizedlinearmaterial.hh

Description

Public Types

Static Public Member Functions

Member Typedef Documentation

◆ Params

◆ Scalar

Member Function Documentation

◆ dpc_dswe()

◆ dswe_dpc()

◆ endPointPc()

◆ krn()

◆ krw()

◆ pc()

◆ sw()