 |
3.1-git
DUNE for Multi-{Phase, Component, Scale, Physics, ...} flow and transport in porous media
|
| |
3.1-git
DUNE for Multi-{Phase, Component, Scale, Physics, ...} flow and transport in porous media
|
A single-phase, isothermal one-equation turbulence model by Spalart-Allmaras. More...
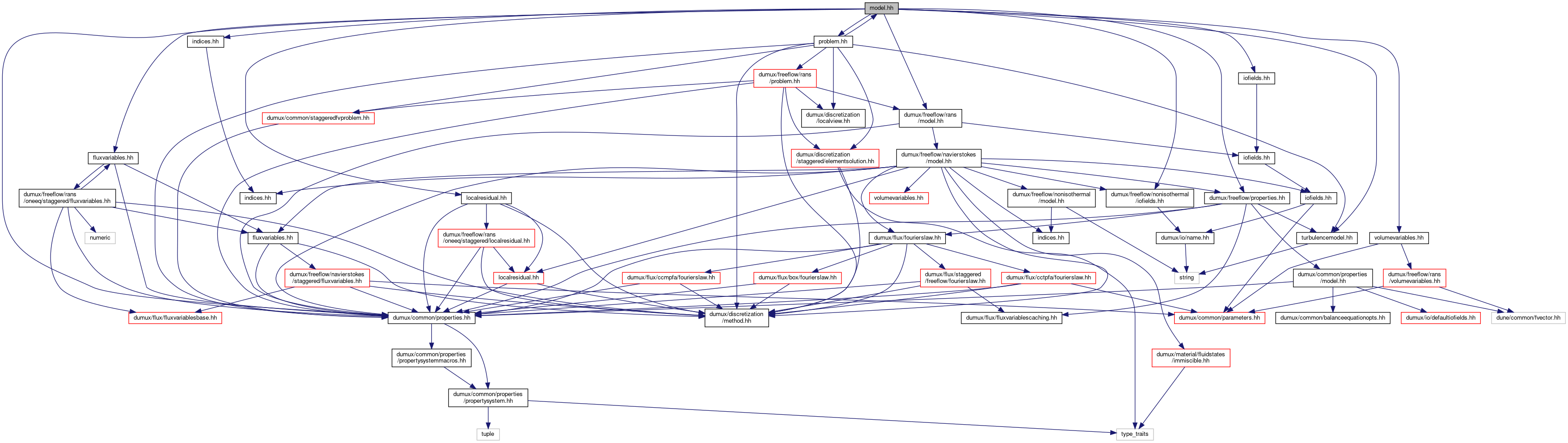
#include <dumux/common/properties.hh>#include <dumux/freeflow/properties.hh>#include <dumux/freeflow/turbulencemodel.hh>#include <dumux/freeflow/rans/model.hh>#include <dumux/freeflow/nonisothermal/iofields.hh>#include "fluxvariables.hh"#include "indices.hh"#include "localresidual.hh"#include "problem.hh"#include "volumevariables.hh"#include "iofields.hh"Go to the source code of this file.
A single-phase, isothermal one-equation turbulence model by Spalart-Allmaras.
Single-phase Reynolds-Averaged Navier-Stokes flow.
This model implements a single-phase, isothermal Reynolds-Averaged Navier-Stokes model, solving the momentum balance equation
\[ \frac{\partial (\varrho \textbf{v})}{\partial t} + \nabla \cdot (\varrho \textbf{v} \textbf{v}^{\textup{T}}) = \nabla \cdot (\mu_\textrm{eff} (\nabla \textbf{v} + \nabla \textbf{v}^{\textup{T}})) - \nabla p + \varrho \textbf{g} - \textbf{f} \]
The effective viscosity is composed of the fluid and the eddy viscosity:
\[ \mu_\textrm{eff} = \mu + \mu_\textrm{t} \]
.
This model, published by Spalart and Allmaras 1992 [64], uses one additional PDE for a working variable \( \tilde{\nu} \). This variable has the units of a viscosity and can be converted to the eddy viscosity via a model function~( \( f_\text{v1} \)):
\[ \nu_\text{t} = \tilde{\nu} f_\text{v1} \]
Here, as proposed by Wilcox [78] and Versteeg [75], the correction term which account for the transition or trip, is dropped from the original equations, such that the balance equation simplifies to:
\[ \frac{\partial \tilde{\nu}}{\partial t} + \nabla \cdot \left( \tilde{\nu} \textbf{v} \right) - c_\text{b1} \tilde{S} \tilde{\nu} - \frac{1}{\sigma_{\tilde{\nu}}} \nabla \cdot \left( \left[ \nu + \tilde{\nu} \right] \nabla \tilde{\nu} \right) - \frac{c_\text{b2}}{\sigma_{\tilde{\nu}}} \left| \nabla \tilde{\nu} \right|^2 + c_\text{w1} f_\text{w} \frac{\tilde{\nu}^2}{y^2} = 0 \]
Here, a modified mean effective strain rate ( \( \tilde{S} \)) based on the mean rotation rate tensor ( \( \mathbf{\Omega} \)) is used:
\[ \tilde{S} = \sqrt{2 \mathbf{\Omega} \cdot \mathbf{\Omega}} + \frac{\tilde{\nu}}{\kappa^2 y^2} f_\text{v2} \]
\[ \mathbf{\Omega} = \frac{1}{2} \left( \nabla \textbf{v}_\text{g} - \nabla \textbf{v}_\text{g}^\intercal \right) \]
This balance equation is linked to the flow geometry by the distance to the closest wall ($y$). Further, the model uses the following functions and expressions:
\[ \chi = \frac{\tilde{\nu}}{\nu} \]
\[ f_\text{v1} = \frac{\chi^3}{\chi^3+c_\text{v1}^3} \]
\[ f_\text{v2} = 1 - \frac{\chi}{1+f_\text{v1}\chi} \]
\[ f_\text{w} = g_\text{w} \left( \frac{1+c_\text{w3}^6}{g^6_\text{w}+c_\text{w3}^6} \right)^\frac{1}{6} \]
\[ g_\text{w} = r_\text{w} + c_\text{w2} (r_\text{w}^6 - r_\text{w}) \]
\[ r_\text{w} = \min \left[ \frac{\tilde{\nu}}{\tilde{S}\kappa^2 y^2},10\right] \]
\[ \sigma_{\tilde{\nu}} = \nicefrac{2}{3} \]
\[ c_\text{b1} = 0.1355 \]
\[ c_\text{b2} = 0.622 \]
\[ c_\text{v1} = 7.1 \]
\[ c_\text{w1} = \frac{c_\text{b1}}{\kappa^2} + \frac{1+c_\text{b2}}{\sigma_{\tilde{\nu}}} \]
\[ c_\text{w2} = 0.3 \]
\[ c_\text{w3} = 2 \]
Namespaces | |
| namespace | Dumux |
| make the local view function available whenever we use the grid geometry | |
| namespace | Dumux::Properties |
| namespace | Dumux::Properties::TTag |
| Type tag for numeric models. | |
1.9.3