 |
3.2-git
DUNE for Multi-{Phase, Component, Scale, Physics, ...} flow and transport in porous media
|
| |
3.2-git
DUNE for Multi-{Phase, Component, Scale, Physics, ...} flow and transport in porous media
|
A single-phase, isothermal low-Reynolds k-epsilon model. More...
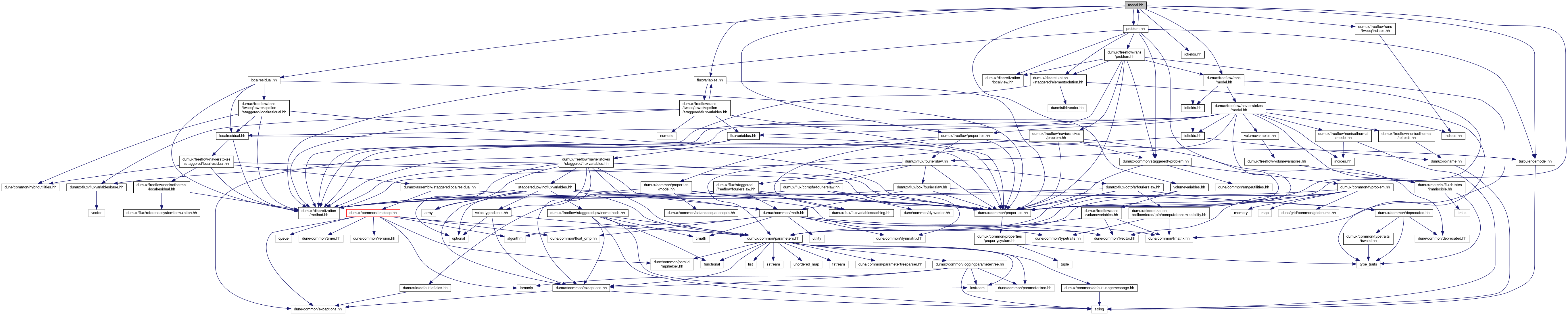
#include <dumux/common/properties.hh>#include <dumux/freeflow/properties.hh>#include <dumux/freeflow/rans/model.hh>#include <dumux/freeflow/rans/twoeq/indices.hh>#include <dumux/freeflow/turbulencemodel.hh>#include "problem.hh"#include "fluxvariables.hh"#include "localresidual.hh"#include "volumevariables.hh"#include "iofields.hh"Go to the source code of this file.
A single-phase, isothermal low-Reynolds k-epsilon model.
Single-phase Reynolds-Averaged Navier-Stokes flow For a detailed model decription see freeflow/rans/model.hh.
The low-Reynolds k-epsilon models calculate the eddy viscosity with two additional PDEs, one for the turbulent kinetic energy (k) and for the dissipation ( \( \varepsilon \)). The model uses the one proposed by Chien [12]. A good overview and additional models are given in Patel et al. [48].
The turbulent kinetic energy balance is identical with the one from the k-epsilon model, but the dissipation includes a dampening function ( \( D_\varepsilon \)): \( \varepsilon = \tilde{\varepsilon} + D_\varepsilon \):
\[ \frac{\partial \left( k \right)}{\partial t} + \nabla \cdot \left( \textbf{v} k \right) - \nabla \cdot \left( \left( \nu + \frac{\nu_\text{t}}{\sigma_\text{k}} \right) \nabla k \right) - 2 \nu_\text{t} \textbf{S} \cdot \textbf{S} + \tilde{\varepsilon} + D_\varepsilon = 0 \]
.
The dissipation balance is changed by introducing additional functions ( \( E_\text{k}\), \( f_1 \), and \( f_2 \)) to account for a dampening towards the wall:
\[ \frac{\partial \left( \tilde{\varepsilon} \right)}{\partial t} + \nabla \cdot \left( \textbf{v} \tilde{\varepsilon} \right) - \nabla \cdot \left( \left( \nu + \frac{\nu_\text{t}}{\sigma_{\varepsilon}} \right) \nabla \tilde{\varepsilon} \right) - C_{1\tilde{\varepsilon}} f_1 \frac{\tilde{\varepsilon}}{k} 2 \nu_\text{t} \textbf{S} \cdot \textbf{S} + C_{2\tilde{\varepsilon}} f_2 \frac{\tilde{\varepsilon}^2}{k} - E_\text{k} = 0 \]
.
The kinematic eddy viscosity \( \nu_\text{t} \) is dampened by \( f_\mu \):
\[ \nu_\text{t} = C_\mu f_\mu \frac{k^2}{\tilde{\varepsilon}} \]
.
The auxiliary and dampening functions are defined as:
\[ D_\varepsilon = 2 \nu \nicefrac{k}{y^2} \]
\[ E_\text{k} = -2 \nu \frac{\tilde{\varepsilon}}{y^2} \exp \left( -0.5 y^+ \right) \]
\[ f_1 = 1 \]
\[ f_2 = 1 - 0.22 \exp \left( - \left( \frac{\mathit{Re}_\text{t}}{6} \right)^2 \right) \]
\[ f_\mu = 1 - \exp \left( -0.0115 y^+ \right) \]
\[ \mathit{Re}_\text{t} = \frac{k^2}{\nu \tilde{\varepsilon}} \]
.
Finally, the model is closed with the following constants:
\[ \sigma_\text{k} = 1.00 \]
\[ \sigma_\varepsilon =1.30 \]
\[ C_{1\tilde{\varepsilon}} = 1.35 \]
\[ C_{2\tilde{\varepsilon}} = 1.80 \]
\[ C_\mu = 0.09 \]
Namespaces | |
| namespace | Dumux |
| namespace | Dumux::Properties |
| namespace | Dumux::Properties::TTag |
| Type tag for numeric models. | |
1.9.3